#1 Deriving the Equal Temperament Tuning System (Part I)

Intro

Edit: the equations render kind of wonky on mobile phones, and in some cases omit plus signs (omg!). I recommend you read this on a laptop or other computer.

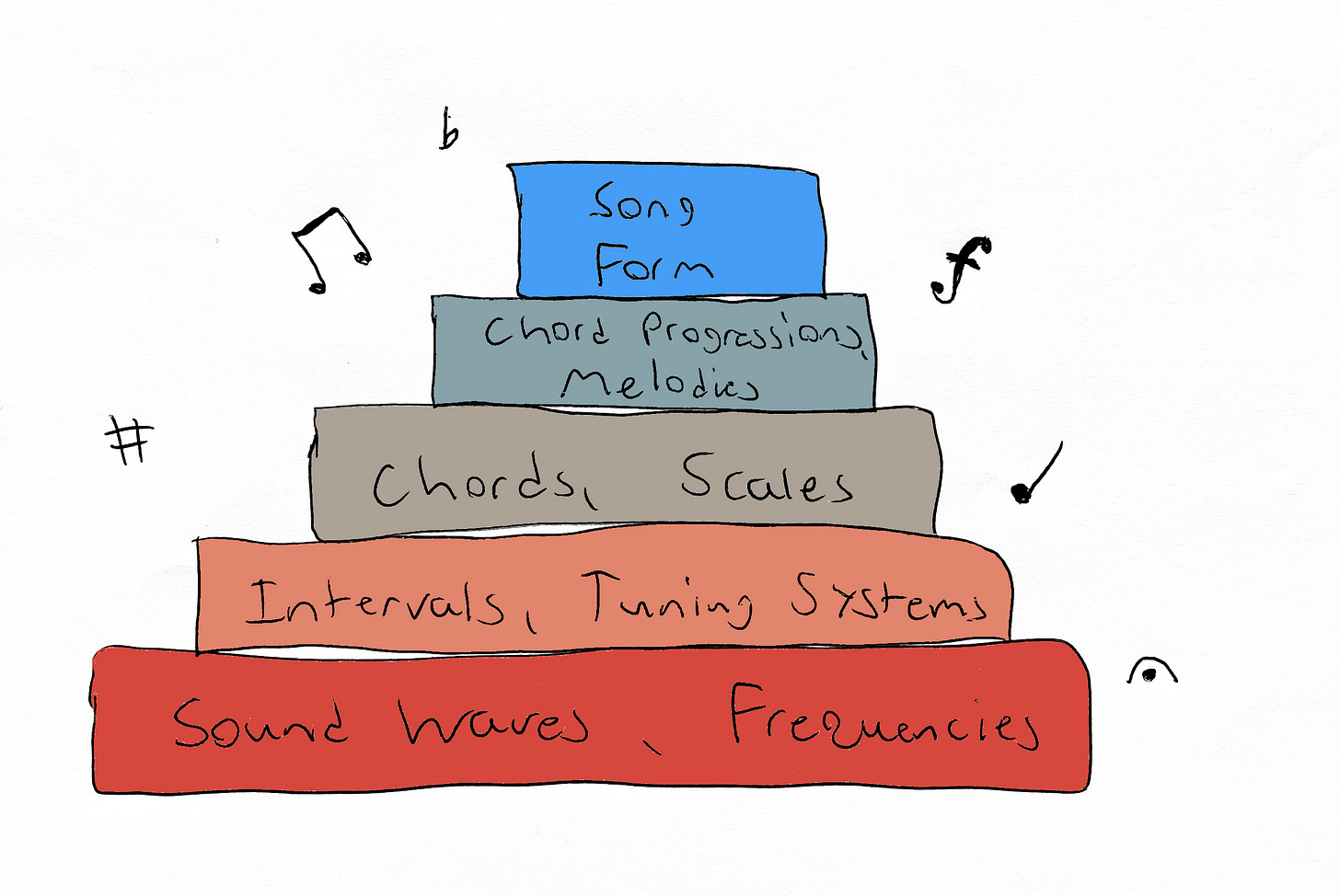
There are many different ways you can look at music analytically, whether you’re trying to come up with new practice exercises, rhythmic patterns, or analyzing harmony. If you picture music theory as several layers of abstraction and building blocks (a familiar idea to computer scientists), I feel the most overlooked levels are the bottom ones.

There are many interesting concepts in the bottom levels, each with their own motivating questions and history. How do sound waves of a certain frequency become classified as one of the 12 notes we use today in Western music? Why do we use 12 notes? Why does the same note sound different on different instruments? What’s the circle of fifths and where does it come from? Why do we have sharps and flats? Why is sheet music drawn the way it is? (I could continue this list all day, there are several interesting things happening here that all tangentially relate to each other).

The specific topic I want to discuss in this blog post is how we turn the frequency spectrum (a continuous domain) into a set of notes to be used by musicians (a set of fixed frequencies, a discrete domain). If you’ve taken some computer science or math classes in college, you might know this problem as quantization.

Why might we want to quantize the frequency spectrum? Suppose you’re trying to write down how to play a song for other musicians. You’d like to be precise with what frequencies you want to use, but being too precise will be difficult for musicians to achieve. No musician will play your song if your melody is “860Hz, 972Hz, …” You’ll need an easier and quicker way to disseminate the information. Also, while string instruments can continuously pass over the frequency domain, brass instruments, woodwinds, and percussive instruments (including the piano) wouldn’t be able to accomplish this (they’re build with a small number of valves, and keys). Quantization of frequencies allows for music to be more easily composed and played.

Problem Statement

For the purposes of this post, I’m going to assume you know how sound waves work and about their basic properties, such as frequency, amplitude, etc. One of the first things you’ll learn when you start exploring the relationships between frequency and pitch is that a frequency f and the frequency 2f sound very similar. Of course, they aren’t the same pitch, but compared to every other frequency, 2f will sound the most similar to f. (0.5f describes the same relationship, if you want to be a stickler). Because of this, we typically assign f and 2f to the same set of pitches and label them with the same “note” name. E.g. f=440Hz and 2f=880Hz are both considered to be included in the set of pitches called “A” in most tuning systems. The acoustic similarities between f and 2f are so strong, actually, that they form the most fundamental relationship between two different frequencies in a tuning system called an octave. We’ll use this fact multiple times.

If you apply this relationship multiple times, you’ll notice that we build a set of exponentially related frequencies:

\(\{f,\ 2f,\ 4f,\ 8f,\ ...,\ 2^nf\}\)

The pleasant acoustic properties of these frequencies with each other reveals an interesting fact: humans experience pitch logarithmically. For the task of converting the continuous frequency domain into a discrete set of pitches, this isn’t just quantization, but quantization in a logarithmic domain, which should be considered when designing a tuning system. As good mathematicians, lets define some of these terms and describe the problem statement more formally.

Humans can only hear frequencies in the continuous domain [20Hz, 20,000Hz], so let that be the limits on our input domain.

\(\text{Let }H=[20, 20000]\)

Let a quantization, or a "tuning system" be a finite set of finite sets of frequencies where no frequency is used twice.

(Need a refresher on your Greek alphabet? See the Wikipedia. I’ll be using capital letters for notes and lowercase letters for frequencies in that note.)

\(Q=\{\mathrm{A},\mathrm{B},\Gamma,\Delta,...\}=\{\{\alpha_1,\alpha_2,...\},\{\beta_1,\beta_2,...\},\{\gamma_1,\gamma_2,...\},\{\delta_1,\delta_2,...\},...\}\)

\(\alpha_1,\alpha_2,...,\beta_1,\beta_2,...\gamma_1,\gamma_2,...\delta_1,\delta_2,...\in H\ \ \ \text{(they're frequencies)}\)

\(\text{Let the elements of }Q\ \ (\mathrm{A},\mathrm{B},\Gamma,\Delta,...)\text{ be called }\textbf{notes}\)

There are several ways we can construct a solution Q, but lets start by defining some properties that would be nice for Q to have. The first property we should consider is the nice acoustic relationship between f and 2f that we discussed earlier.

Property 1 - The Octave Property:

\(\text{Let }\ \ \alpha_{i+1}=2\alpha_i\ \ \ \ \ \beta_{i+1}=2\beta_i\ \ \ \ \ \gamma_{i+1}=2\gamma_i\ \ \ \ \ \delta_{i+1}=2\delta_i\ \ \ \ \ ...\)

\(\text{Let }f^*\text{ be called an }\textbf{octave }\text{of }f\text{ if }\ \ \ f^*=2^af\ \ \text{for any integer }a\)

You’ve probably heard about octaves before, and you might even be familiar with this mathematical relationship already. No tricks here.

You might wonder why we’re defining the property within sets instead of across sets. If you define it this way, you’ll reach the same solutions as the first definition, just with the frequencies renamed. Leave a comment if you want to know more! But for now, lets just use this definition.

Property 2 - Octave-Proof Intervals:

Let a function from one frequency to another be called an interval. Melodies are constructed with several notes, each with their own intervals between them. For several reasons, such as arranging for other instruments, or just transposing up and down octaves, it would be nice for us to play the same melody in different octaves without the melody becoming distorted. In other words, changing the octave should not change the interval function. Here’s that written mathematically:

\(2V(f)=V(2f)\text{ for some interval function }V(f)\text{ over frequencies }f\in H\)

First, realize that this property is not true for all interval functions:

\(\text{Let }V(f)=f+1000\)

\(2V(f)\neq V(2f)\)

\(2f+2000\neq 2f+1000\)

So what functions V(f) satisfy this property? Well it turns out that answering this question will help define our tuning system Q.

Solving for the Interval Function V(f)

Property 2 is a property of the function V(f), known as function homogeneity. A function f(x) is homogeneous to degree k if

\(f(sx)=s^kf(x)\ \ \ \ \ \text{for some integer }k\text{ and scalar }s\)

If you’re interested, you can read more about homogeneous functions on Wikipedia (which is pretty reliable for math in my experience). For us, I’ll pull out the interesting line from the article:

\(\text{“The homogeneous real functions of a single variable have the form }𝑥↦𝑐𝑥^𝑘\text{ for some constant }c.\text{”}\)

This statement describes homogeneity for degree k. In our case though, we’re only interested in homogeneity of degree k=1. So, if our interval function can be written as

\(V(f)=cf\)

then the question becomes: what values can c be and still satisfy Property 1? To answer this question, lets look at what happens to frequencies undergoing this interval function multiple times.

Compounding Intervals

Let’s revisit the definition of our tuning system Q and add in some details. Remember that Q is a finite set of sets called notes. Let’s label the sets starting with A and having each successive note be the result of the interval V:

\(\text{Let }V(\alpha_0)=\beta_0\text{ for some }\alpha_0\in\mathrm{A}\)

You can use the both Properties 1 and 2 of our tuning system to show that this is true for all frequencies in A:

\(\alpha_1=2\alpha_0\longrightarrow V(\alpha_1)=V(2\alpha_0)=2V(\alpha_0)=2\beta_0=\beta_1\)

\(V(\alpha_i)=\beta_i\ \ \text{ for all }\ \ \alpha_i\in\mathrm{A},\beta_i\in \mathrm{B}\)

Continuing this pattern, we can see that Q looks like this:

\(V(\alpha)\in\mathrm{B}\ \ \ V(\beta)\in\Gamma\ \ \ V(\gamma)\in\Delta\ \ \ ...\)

\(Q=\{\mathrm{A}\overset{V}{\rightarrow}\mathrm{B}\overset{V}{\rightarrow}\Gamma\overset{V}{\rightarrow}\Delta\overset{V}{\rightarrow}...\overset{V}{\rightarrow}\Psi\overset{V}{\rightarrow}\Omega\}\)

where Ω is our last note. Each iteration of our interval gives the next note! Let’s introduce some notation for applying this interval function several times in a row.

\(\text{Let }V^n(f)=\underbrace{V(V(...V(f)))}_{n\text{ times }}=c^nf\)

Now, back to Q. What happens when we apply our interval to Ω ? Because Q is finite and because Ω is the last note, then applying V to Ω must give us a note we’ve already seen. Let’s consider 3 cases of what V(Ω) might be. Our 3 possible cases are

\(V(\omega)\in\mathrm{A},\ \ \ \ V(\omega)\in\Theta,\ \ \ \ V(\omega)\in\Omega,\ \ \ \ \ \ \ \text{ for all }\omega\in\Omega\)

Where Θ is another note in Q besides A and Ω . The third case is actually really boring because it just means that our interval function is some number of octaves:

\(V(\omega)\in\Omega\longrightarrow V(\omega)=2^n\omega\ \ \ \ \text{ for }n\text{ number of octaves}\)

\(\text{This also means }\mathrm{A}=\Theta=\Omega\ ,\ \ \ \ Q=\{\Omega\}\)

A tuning system with only one note won’t make for very interesting music, so let’s consider the two other cases! Let’s rewrite Q as

\(Q=\{\mathrm{A}\overset{V^n}{\rightarrow}\Theta\overset{V^m}{\rightarrow}\Omega\}\)

\(\text{If we start constructing }Q\text{ with the frequency }\alpha_0,\text{ then lets define the frequencies }\)

\(V^n(\alpha_0)=\theta\ ,\ \ \ V^m(\theta)=\omega\ \ \longrightarrow\ \ V^{n+m}(\alpha_0)=\omega\)

Let’s first consider the case where V loops back to A:

\(\text{If }V(\omega)\in\mathrm{A}\text{, then }V(\omega)=2^a\alpha_0\longrightarrow V(V^{n+m}(\alpha_0))=2^a\alpha_0\)

\(V^{n+m+1}(\alpha_0)=2^a\alpha_0\ \ \longrightarrow \ \ c^{n+m+1}\alpha_0=2^a\alpha_0\ \ \longrightarrow \ \ c^{n+m+1}=2^a\)

Basically, this is saying that after applying V n+m+1 times, you get the same frequency as if you had just gone up a octaves! There’s still the mystery of what our multiplying constant c is, but lets consider the other case first.

\(\text{If }V(\omega)\in\Theta\text{, then }V(\omega)=2^b\theta\longrightarrow V(\omega)=2^bV^n(\alpha_0)\)

\(V(\omega)=2^bV^n(\alpha_0)\ \ \longrightarrow\ \ V(V^{n+m}(\alpha_0))=2^bV^n(\alpha_0)\)

\(V^{n+m+1}(\alpha_0)=2^bV^n(\alpha_0)\ \ \longrightarrow\ \ c^{n+m+1}\alpha_0=2^bc^n\alpha_0\)

\(c^{m+1}\alpha_0=2^b\alpha_0\ \ \longrightarrow\ \ c^{m+1}=2^b\)

This is a very similar result. We can see that if you apply V n+m+1 times, you get the same frequency as if you had applied V n times, and then gone up b octaves. Also take note that in both cases, our original frequency α0 doesn’t even matter! Now, let’s take these two results and determine what c is.

Determining the Interval Function

Because n, m, a, and b are all positive integers (they’re the # of times we’ve applied V or # of octaves) then both of our results are of the form

\(c^\text{some +integer}=2^\text{some +integer}\)

Let’s call these integers p and q. In order to determine what c is, it doesn’t really matter what they are right now.

\(c^q=2^p\)

We can do a simple operation to finally solve for c:

\((c^q)^{\frac{1}{q}}=(2^p)^{\frac{1}{q}}\ \ \ \ \longrightarrow\ \ \ \ c=2^\frac{p}{q}\ \ \ \ \longrightarrow\ \ \ \ V(f)=2^{\frac{p}{q}}f\)

Note that while we haven’t come up with p and q, we have shown that c is 2 raised to a rational number. In fact, this actually says that in order to achieve both of the desirable properties discussed earlier, 2 raised to any rational number will work, which gives us many different options for V(f)! This might be a bit of a disappointment for some of you that were hoping for me to come up numerical value for c. As a consolation prize, I’ll make a Part II to this post discussing good choices for p and q and their effects on Q (this post is getting too long anyways).

Next Steps

Part of the fun of exploring things analytically is that solving one problem often leads to more questions to be explored (the fun never stops!). While this post gets very specific about V(f), we should remember that this is a very specific piece of the larger musical puzzle. Notice that apart from telling you that octaves (f and 2f) sound good together, I haven’t made any other points about how things sound under a tuning system with these properties. Here are some more questions you might be wondering about

• Will f and V(f) even sound good together?

• The title of this post is “Deriving the Equal Temperament Tuning System”. What even is Equal Temperament?

• Are there other ways to come up with a tuning system (a quantization)?

• I thought music was supposed to be fun, why’s he brought math into this? 😛

Next time I’ll pick up where I left off and help paint a more complete picture of what our result here has shown us. Hopefully we’ll be able to answer all of these questions. Feel free to leave a comment if you have a question of your own you’d like answered. Thanks for reading, and subscribe!